| |
索瑪立方體是由丹麥皮亞特‧海恩 (Piet Hein) 發明的。1933年[1]他在聆聽德國物理學家偉納‧海森伯格 (Werner Heisenberg) 演講
“量子物理” 的場合，在海森伯格講論某種空間切割合成立方體的問題時，海恩豐富的想像力立刻捕捉到這些奇異的幾何概念，
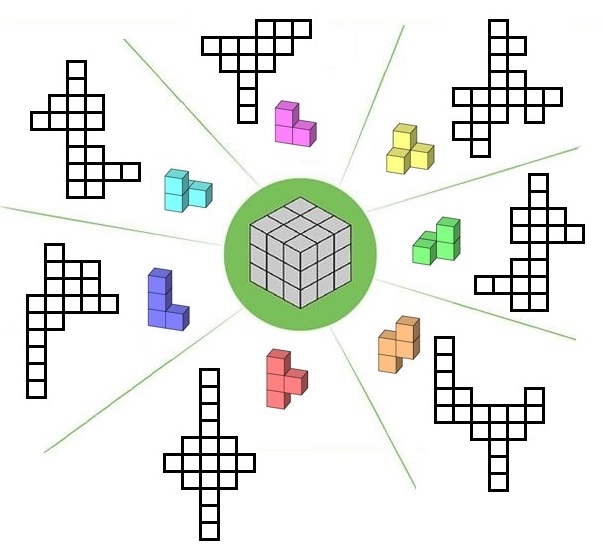
構思出索瑪立方體 - 基於一個由3個同樣大小的立方體做出的不規則立體(下圖第 1 個立體)，然後將第4個立方體附上，
做出6種不規則形狀立體，其中有兩個是互相鏡像對稱的(下面第二圖中的第1號和第5號立體)，這7 個不規則形狀立體，
很可能組合出一個 3 X 3 X 3 的大立方體。就在海森伯格的課堂完結後，海恩立刻用 27 個立方體，按他的構想，
用膠水黏合出這7 個不規則形狀立體來，再組合出一個大立方體，並確定他的洞察力是對的。
基於一個由3個立方體做成的立體，將第4個立方體附上，做出 6 種不規則形狀立體
|
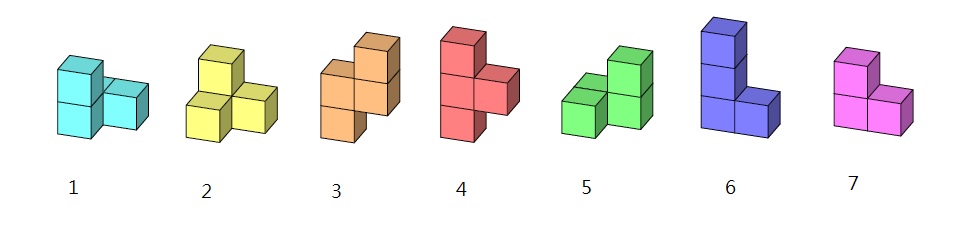組成索馬立方體的 7 個不規則立體塊
|
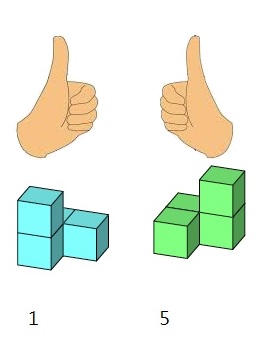鏡像對稱可用左手和右手旋轉系統來區分
|
海恩稱這個立方體為索馬 (SOMA)，並將他這個索馬立方體的想法於1934年在英國申請註册[2]，交給多家製造商製造，
製造商埃里克‧威勒姆森 ( Erik Willumsen) 造出木製的原始索馬立方體。1967年海恩與西奧多‧斯科德 ( Theodor Skjøde) 合作，
發行那十分美麗鋁金屬座紅木 (Rosewood) 索馬立方體；在美國， 派克兄弟公司 (Parker Brother Inc.) 也發行了紅色和藍色兩款塑膠索馬立方體，
至1999 年也開始有用摺紙、發泡膠、卡紙盒和用骰子黏合的索馬立方體版本。
尼爾斯‧玻爾(Niels Bohr)(中)、海森伯格(前右)和海恩(後中)，1930年
|
斯科德坐在他花園裡的大型索馬立方體上
|
威勒姆森公司製造的索馬立方體
|
海恩給這個立方體取名 SOMA，名字源於奧爾德斯‧赫胥黎 (Aldous Huxley) 於1931年出版的書《美麗新世界》( Brave New World )
中所提到的一種無副作用而予人及時福樂的神經製劑藥物名稱。
馬丁‧加德納 (Martin Gardner) 在美國科學人 (Scientific American) 雜誌的文章(September 1958, pp182-196)[3]
介紹索馬立方體時，他以為讀者很難造出一套索馬立方體，但他估計錯誤，過千以上的讀者向他投訴這個索馬立方體花耗了他們的休閒時間，
並寄上新索馬繪圖，教師們給他們班課做索馬立方體，心理學家也把索馬立方體列於其心理測試表中。
索馬立方體擁躉更是造多套作為聖誕禮物送給在醫院中的朋友，寶石顏色公司(Gem Colour Company)
得到海恩的授權，製成商品在市場發售。
數學遊戲(Mathematical Games)
科學美國人(Scientific American) 1958年九月號
|
弗雷德里克‧阿洛伊斯‧弗里德爾 (Frederic Alois Friedel 1945年出生，科學記者，ChessBase 的聯合創始人，
曾在漢堡大學和牛津大學學習哲學和語言學) 在少年時因為加德納這關於索馬立方體文章而開始玩和設計圖形給別人，
其中一個設計也曾獲奬[4]。
弗里德爾少年時投稿到雜誌社的設計原圖
|
下面是玩索馬立方體最基本的幾個練習︰
(1) 試找出 2 個索馬立方體組件來組合出下面形狀的立體。
(2) 試用除了第 7 號立體外的其餘 6 個立體做出與第 7 號立體同形狀的立體，只是邊長是它的兩倍。
做完上面的練習後，就試試找出用全部 7 個立體塊組件去組合出索馬立方體。
我們知道在將 7 個立體塊去組合索馬立方體時，若第一個放不對位，就注定做不成，
但很多時我們要放多一兩個立體塊才會發覺，所以如何放第一個立體塊就很重要了。
索馬立方體有 8 個角位，那麽這 7 個索馬立體塊有多少置法是佔據這些角位的呢[5]？
我們發現第 6 號立體塊可佔 0 、1 或 2 個角位，第 4 號可佔 0 或 2 個角位，第 3 號 和第 2 號佔 0 或 1 個角位，其餘的也是佔 0 或 1 個角位。
由此可以看到若第 4 號立體塊 ( ‘ T ‘ ) 不佔角位，則其餘立體塊最多只能佔 7 個角位，
因此立體塊 ' T ' 也只能得一種佔據 2 個角位的置法。
另外我們也可從著色法來分析。
將 3 X 3 X 3 索馬立方體用棋盤著色法塗上紅色和黑色，我們特意將 8 個角塗成紅色，以便說明。
此時的索馬立方體有 14 個紅色小立方體和 13 個黑色小立方體。
首先，第 1、3、5 和 6 號立體塊就只能是 2 黑 2 紅。
因為第 4 號立體塊 ‘ T ‘ 佔據兩個角，所以一定是 3 紅 1 黑。
第 2 號立體塊是 3 紅 1 黑 或是 3 黑 1 紅。若是 3 紅 1 黑的話，在未加上第 7 個立體塊時，就已有 14 個紅色小立方體，
不合，所以第 2 號立體塊是 3 黑 1 紅。因此若此立體要佔據索馬立方體的一角，必然是這立體塊角位上紅色小立方體。
因為已有 12 紅 12 黑，所以第 7 號立體塊必然是 2 紅 1 黑，黑色在角位。所以若這立體塊要佔據索馬立方體的角位時，
一定不是角位上這黑色小立方體。
明白這些小提示，我們可以試找出一個解法。
第一個放上的是第 4 號立體塊 ( ' T ' ) ，再放第 6 號立體塊 ( ' L ' )。
再用第 2 號立體塊 ( ' Q ' ) 充填底層留下的空位。
此時第 3 號立體塊 ( ' S ' ) 有 3 種放法，第 2 種(中)放法留下一空隙，不取。我們就試採用第 1 種(左)放法，然後繼續放下立體塊。
第 1 號立體塊的可能置法中，只有第 1 種 (左) 的放法可行。
餘下的兩個立體塊的放法就很自然了。
索馬立方體解法，若包括反射對稱、旋轉等，共 1105920 種，這結果是經由約翰‧H‧康威 ( Dr. John H. Conway)
和 M.J.T. 蓋伊 ( Dr. M.J.T. Guy) 用電子計算機分析出來的。加州科技機構 (California Institute of Technology)
的 N.S. 紐霍爾 ( N.S. Newhall ) 用 IBM 7094 電子計算機花 82 秒時間便把解答打印出來，並由其他幾位科學家核證。
但若除去鏡像對稱、旋轉，可組合成立方體的解答有 240 種。但其中的第 1 號立體塊和第 5 號立體塊是鏡像對稱立體，
若我們視他們對調所組合出的索馬立方體是不同做法的話，就該有480種解答[6]。
用索馬立方體組件可以拼出很多活靈活現，造型生動的立體圖形，在這裏我選出幾款馬丁‧加德納文章中的索馬圖形給大家，
好讓大家能在買到或自做了索馬立方體後動動腦筋。
除了跟着圖形找解答外，大家亦可自行設計，或到網上尋找更多索馬圖形[7]。若用兩套索馬立方體組件來玩，
變化和挑戰更大，樂趣更多。下面的圖形 Three Ways Out (索馬立方體說明書內的例子, 1969) 是個用兩套索馬立方體做出來的圖形。
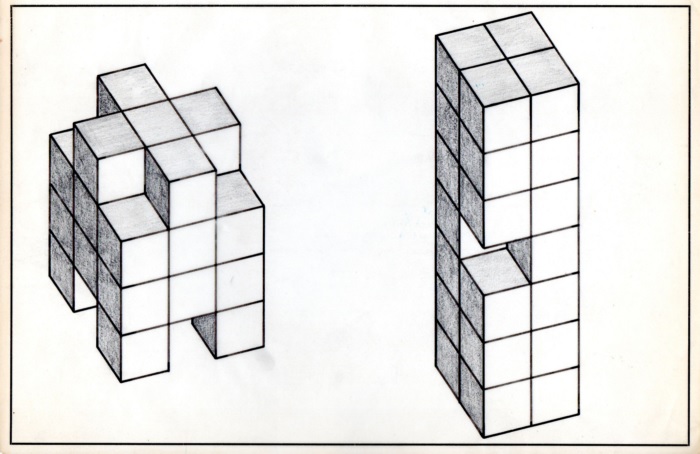
不是所有繪出來的索馬圖形都能拼做出來，就如上面的摩天大廈，是不能做出來的。
摩天大廈，是不能用索馬立方體做出來的
|
另外，下圖是一個著名例子，所羅門‧W‧戈隆 (Solomon W. Golomb ) 已證明這索馬圖形不能做出來。
在玩索馬立方體之餘，也跟大家談些有關的趣聞。
林凱毅 (Lim Kai Yi) 是位熱心於快速度解問題的人，他其中一個目標是索馬立方體。 2021 年 3 月他在馬來西亞檳城威省的北海 (Butterworth)
只用了 2.458 秒的時間就完成索馬立方體的組合，是個紀錄[8]。
2012 年 12 月美國紐約數學博物館 (National Museum of Mathematics) 舉辦一項展覽活動[9]，一群參與者用 216 個邊長 2 呎的立方紙盒，
以 8 個紙盒用膠紙黏合成一立方體單元，然後用這些立方體單元做出索馬立方體的 7 個立體塊，展出並拼出不少索馬圖形。
想玩索馬立方體，當然要有一套才行。最簡單直接的方法，就是去玩具店或網上購買，但也可以自己製做。
若果想自己製造一套索馬立方體，可以去平價店或手工藝店買包小木立方體，然後用白膠漿黏合出索馬立方體的 7 個立體塊。
又或者可以用紙畫出這 7 個立體塊的網絡圖 [10]，剪下摺合做出來。亦可考慮用 摺紙的方法，摺出 27 個小立方體，黏合出這 7 個立體塊。
用小木立方體自製索馬立方體 (網上圖片)
|
索馬立方體的7 個立體塊網絡圖
|
基本立方體摺法
|
用摺紙方法做出索馬立方體的 7 個立體塊
|
有了一套索馬立方體，我們可做些練習，下面是幾款簡單的索馬圖形給大家嘗試。
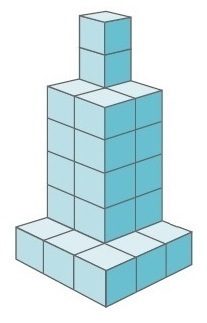
當對索馬立方體有了相當認識後，可以抽象思考一些問題。馬丁‧加德納用索馬立方塊做出的井有多深呢？
(2) 做出雙倍厚度的第 4 號立體塊是用第 5 號和第 6 號立體塊合成。
放大立體問題的解答。
(3) 馬丁‧加德納提供的索馬圖形解答如下：
Three Ways Out 的解答：
(4) 練習的解答：
(5) 井深的問題：
因為做出井的小立方體數目已是 27 ，所以圖形中心是空的，即井的深度是 3 小立方體的高度。
(6) 索馬立方體、魔鬼立方體、格里邦瓦爾立方體和米庫辛斯基立方體的解答：
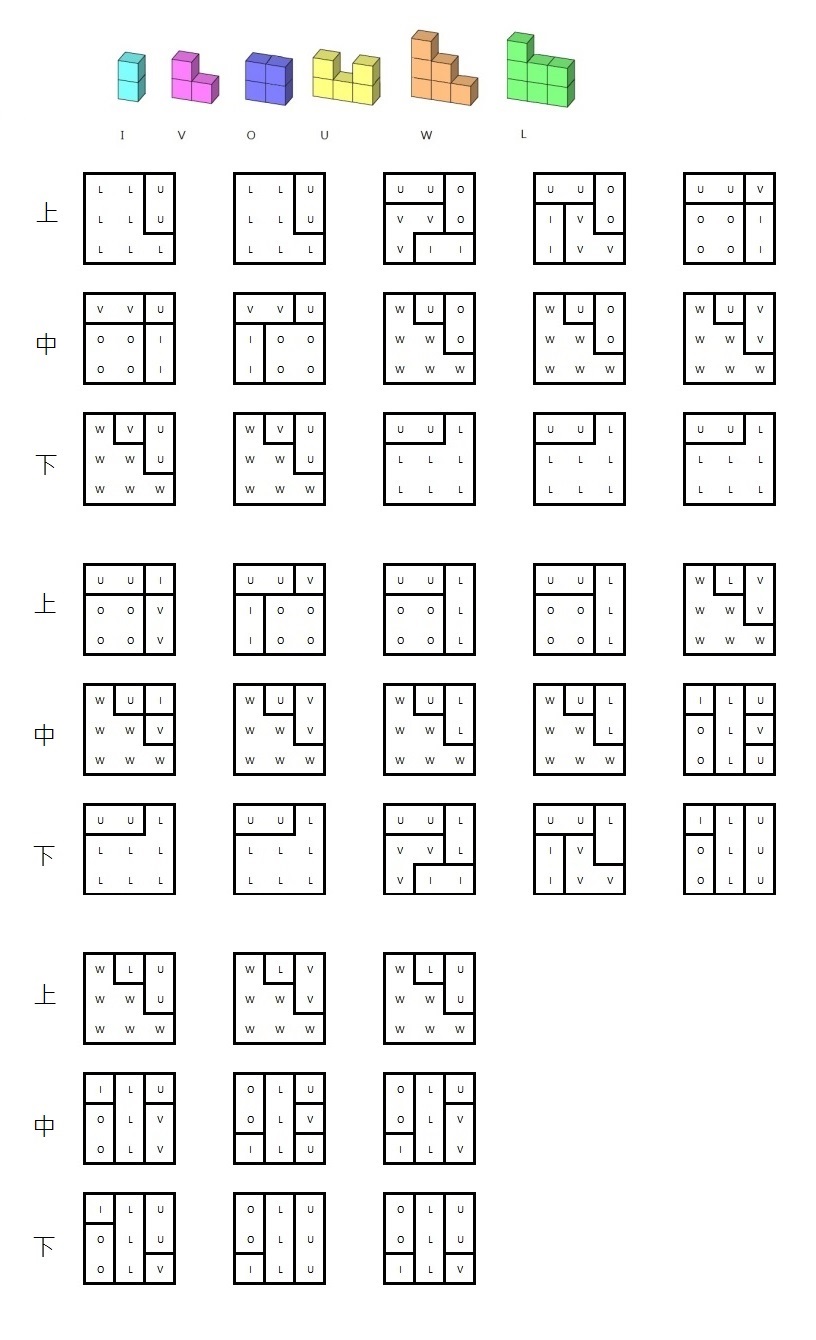
| 索馬立方體的解答[11]： |
 |
 |
 |
 |
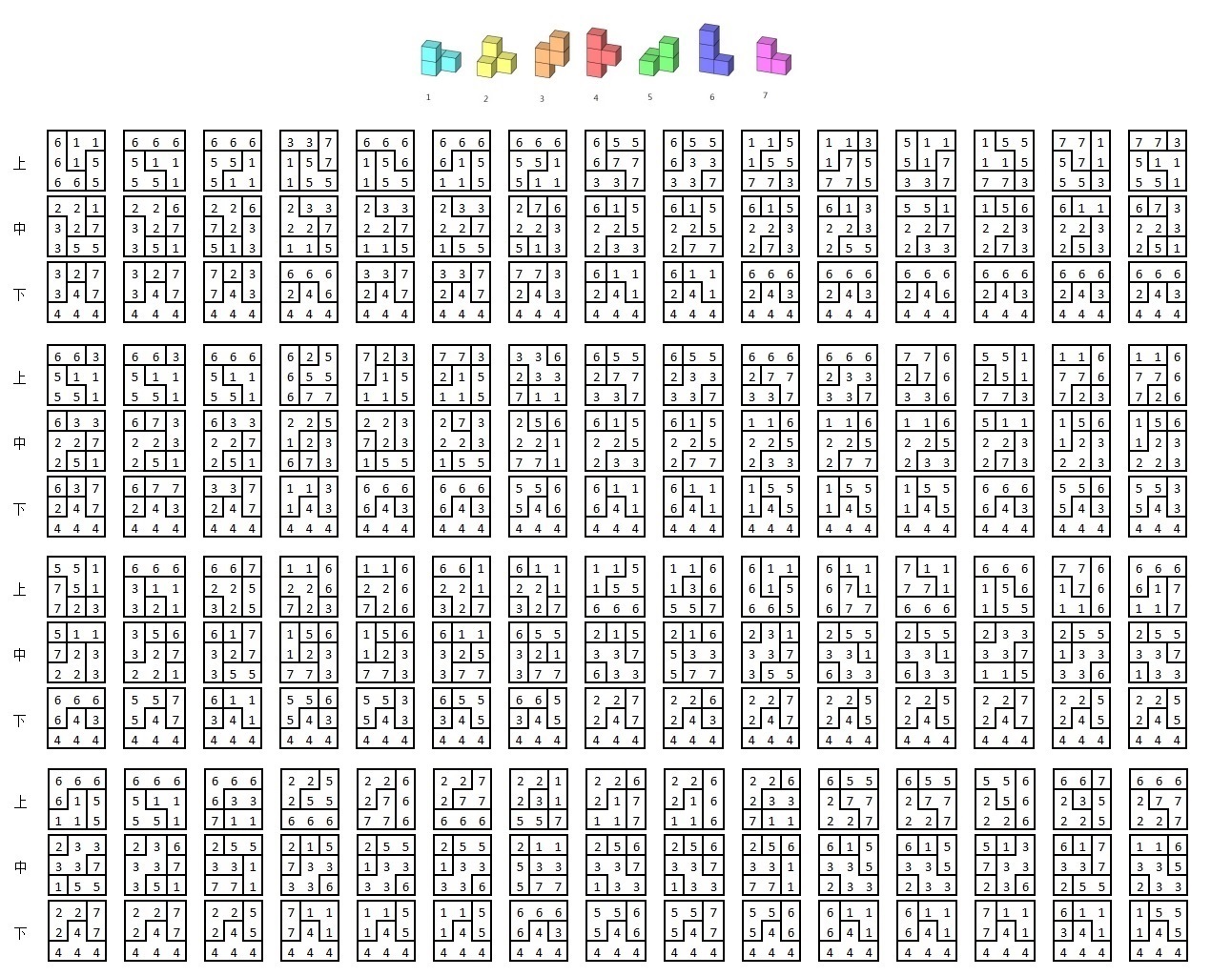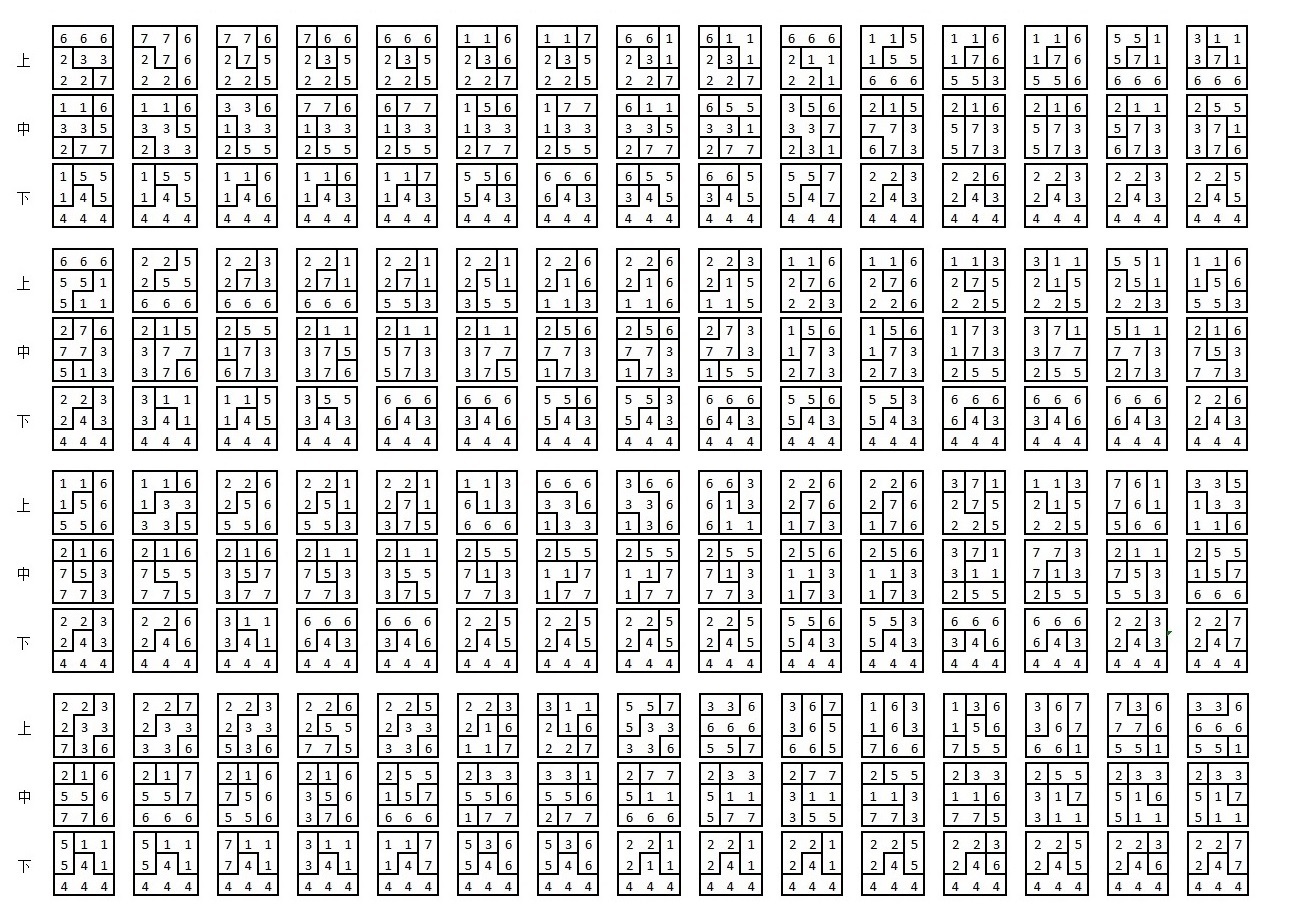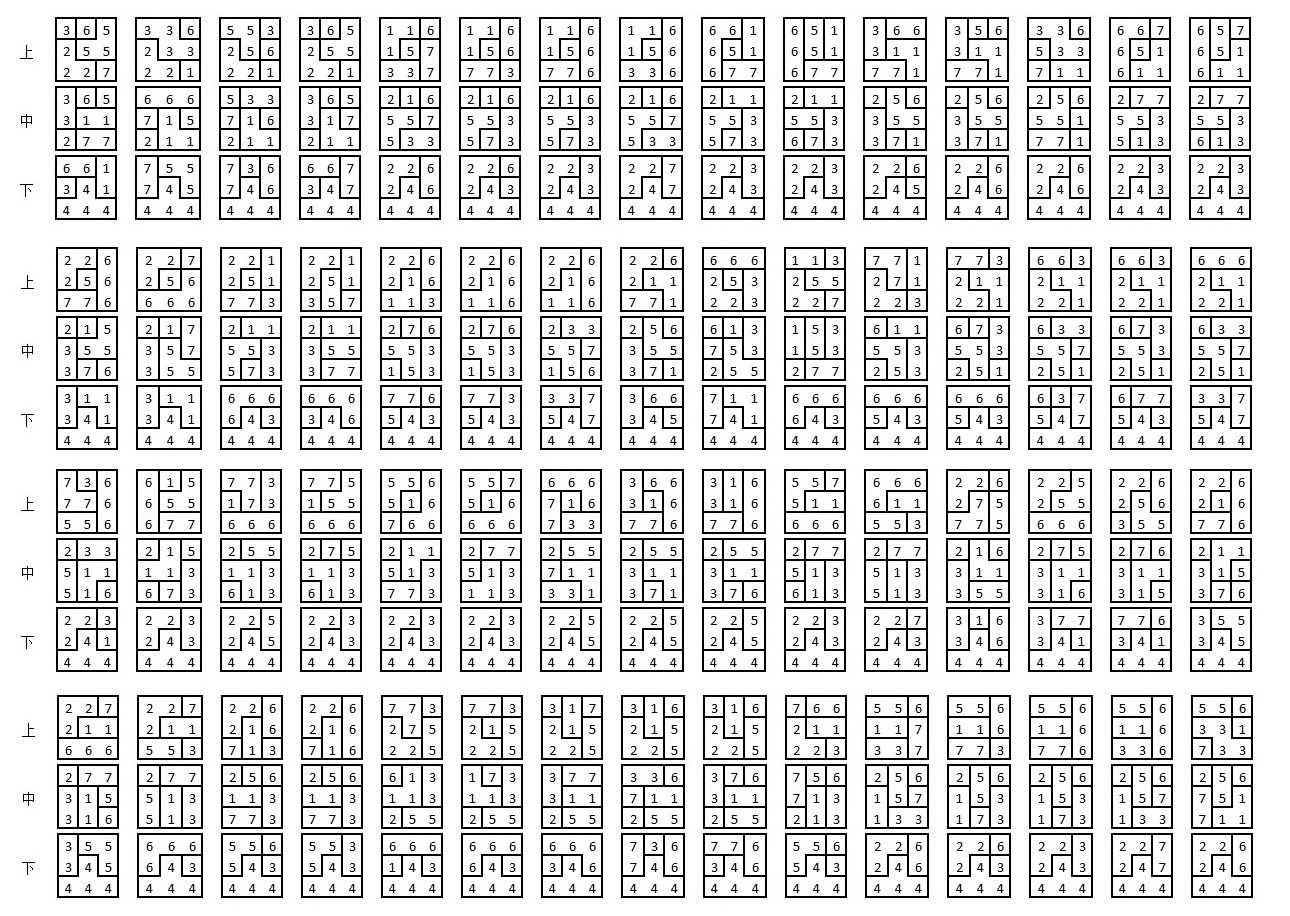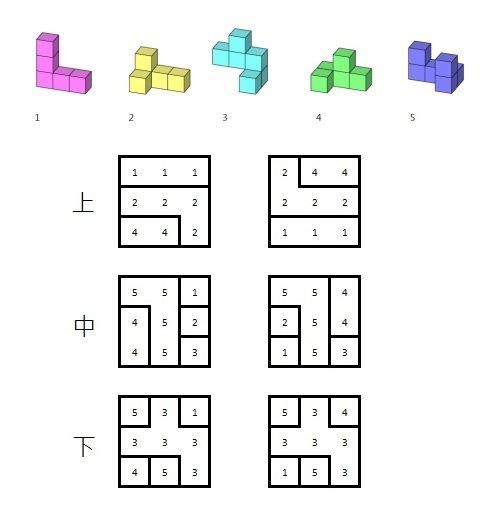
| 魔鬼立方體的解答[12]： |
 |
| 格里邦瓦爾立方體的解答： |
 |
| 米庫辛斯基立方體的解答︰ |
 |
參考資料
| [1] |
|
The birth of SOMA ? |
| |
https://www.fam-bundgaard.dk/SOMA/NEWS/N030310.HTM |
| [2] |
|
Hex, Inside and Out The Full Story, Ruan B. Hayward, Bjarne Toft, CRC Press, 2019, p.3-4 |
| [3] |
|
Scientific American, September, 1958 |
| |
https://quantumneuroscience.ai/papers/The_Physiology_of_Imagination-Scientific_American_1958.pdf |
| [4] |
|
Piet Hein and the Soma Cube |
| |
https://frederic-38110.medium.com/piet-hein-and-the-soma-cube-28680c036268 |
| [5] |
|
The Soma Puzzle Book A New Approach to the Classic Pieces, David Goodman and Ilan Garibi, World Scientific, 2019, p.xiii-xxi |
| [6] |
|
索瑪立方塊 (Soma Cube) |
| |
http://www.chiuchang.com.tw/toy/somacube.html |
| [7] |
|
Soma Figures |
| |
https://www.fam-bundgaard.dk/SOMA/FIGURES/FIGURES.HTM |
| [8] |
|
Fastest time to complete a Soma Cube |
| |
https://www.guinnessworldrecords.com/world-records/435864-fastest-time-to-complete-a-soma-cube |
| [9] |
|
Giant Soma Puzzle |
| |
https://momath.org/activities/giant-soma-puzzle/ |
| [10] |
|
《挑戰索瑪立方體》立體空間思維，從幼升小一直玩到小升初 |
| |
https://kknews.cc/education/lvkxj92.html |
| [11] |
|
All solutions of the Soma cube |
| |
https://www.sciencedirect.com/science/article/pii/0012365X85901608 |
| [12] |
|
Solving Diabolical Cube |
| |
http://puzzler.sourceforge.net/solutions/cubes/diabolical-cube.txt |
相關閱讀
| (1) |
|
More Mathematical Puzzles and Diversions, Martin Gardner, Penguin Books, 1977, p.50-59 |
| (2) |
|
The Second Scientific American Book of Mathematical Puzzles and Diversions, Martin Gardner, The University of Chicago Press, 1987, p.65-77 |
| (3) |
|
Knotted Doughnuts and Other Mathematical Entertainments, Martin Gardner, W.H. Freeman and Company, p.28-p43 |
| (4) |
|
Origami, Eleusis, and the Soma Cube, Martin Gardner, Cambridge University Press,2008, p.51-65 |
| (5) |
|
The Colossal Book of Mathematics, Martin Gardner, W.W. Norton & Company, 2001, p.398-408 |
| (6) |
|
Winning Ways for your Mathematical Plays, Volume 4, Second Edition, Elwyn R. Berlekamp, John H. Conway, Richard K. Guy, A K Peter Wellesley Massachusetts, p.846-847 |
|
|
